|
多分学生時代に係決めや席決めなんかで、あみだくじをした経験はあると思う。
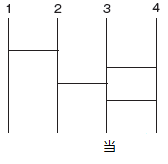
まあ、こういったものだ。この場合、どこを選べばよいか、そんなの3に決まっている。ちょうど当たりの上に位置している。今の場合それは偶然であるが、確率論的に言えば偶然ではない。結論を先に言おう。すべてのあみだくじにおいて、一番当たりやすいのは当たりの真っ直ぐ上の位置である。
これは単純な場合をイメージしてもらえば理解しやすい。まず縦棒が100本あるあみだくじを考えよう。このとき、横棒が1本もなければ、そのあみだくじでは当たりの真っ直ぐ上しか当たりようがない。次に、横棒が一本の場合、当たりの縦棒とその左右どちらかの縦棒の間に引かれない限り、やっぱり真っ直ぐ上が当たりである。当たる確率は大体98/100=49/50と、かなりの確率である。一般的に、横棒の数が大きくなるほど、当たりの確率はどの位置も平均化されていくが、それでも真上が最大になることに変わりない。
ここから少し数学的な考察をする。このあみだくじは、出発点から下って行き、横棒の数だけ、(左、右、そのまま)の判定をくぐることになる。これはコイントスによる1次元のランダムウォークの確率分布と類似している。横棒の数が十分多ければ、これは正規分布に漸近し、平均が真下、標準偏差が通過する横棒の本数の期待値の平方根になる。
ではどのくらい横棒が多ければ、不公平にならないレベルになるだろうか。一つの指標がwikipediaにあったので紹介しておく。標準偏差とは、確率のばらつきを示す変数でこれが大きいほど確率は一定といっていい。もっと言えば、確率の減少の緩急が切り替わる場所までの距離といっていい。今の場合、縦棒がN本、横棒がn本あるとして、標準偏差σがN-1より大きければ妥当と考えられる。1本の横棒に着目するとN人中2人がその横棒を通過するので
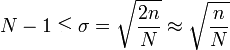
の不等式を解いて、
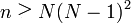
という式が得られた。N=5、つまり縦棒が5本あるあみだくじで考えると、横棒が大体90本以上は必要と示唆している。しかし、現実世界でそんなぎっしり書かれたあみだくじは見たことがない。結局のところ、当たりの真上の優位性は崩れない。
まあ、下部分を全部隠してしまったあみだくじもあったりするのだが、その場合は当たりを書く役に抜擢されていると素敵です。つまり、委員長。ここに委員長最強説が誕生してしまったようです。当たりの位置を把握し、公平を期すと言ってほかの生徒に横棒をひかせつつも、自分はちゃっかり当たりの真上の位置をキープ。そんな委員長がいれば、そのクラスは安泰です。
|